Graph Machine Learning #1 - GNN (Stanford CS224W)

본 블로그는 Stanford의 'CS224W: Machine Learning with Graphs'를 요약한 글임을 밝힙니다.

출처:http://web.stanford.edu/class/cs224w/

CS224W | Home

0. 용어 정리

• V: Vertex/Node set (노드 집합)
  • v: V집합 내 특정 노드 
  • N(v): v노드의 이웃 노드 집합 
• A: Adjacency matrix (인접 행렬)
• Node features는 아래와 같이 표현한다. 

$$ X ∈  R^{m * |V|} $$

• Node Features의 예시는 아래와 같습니다. 
  • 소셜 네트워크(Social Networks): 유저 프로필, 유저 이미지
  • 생물학적 네트워크(Biological Networks): 유전형질 프로필, 유전 함수 정보
• Node Feature가 그래프 Dataset에 없는 경우 아래와 같이 표현합니다. 
  • Indicator vectors (노드 one-hot encoding)
  • 1의 상수 vector([1,1,...1])

---

1. Network 기본 개념

1) Tasks on Networks 

• Node Classification
  • 특정 노드 타입 예측
• Link Prediction
  • 노드간 연결 관계 예측
• Community detection
  • 밀집 노드 군집(densely-linked cluster) 분류
• Network Similarity
  • 두 sub-network간 유사도 판단

2) Network 모델 활용이 어려운 이유

• 대부분의 ML 모델들은 정형적인 Grid Dataset(Image) 혹은 Sequential Dataset(Text/Speech)를 사용한다.
• Graph Dataset은 정형적인 모양을 띄고 있지 않다.
  • No ordering (순서 없음)
  • No reference point (시작 지점 없음)
  • Often Multimodal features (다양한 종류의 데이터 타입이 혼재됨)

---

2. Deep Learning for graphs

1) 시도1 - Naiive approach (DNN)

• 그래프를 인접 행렬(adjacency matrix)로 표현하여 DNN에 feed forward하는 방식
• 문제점
  • O(|V|)만큼의 파라미터를 갖음 
  • 다른 크기의 그래프에 적용할 수 없음
  • 순서에 민감함

2) 시도2 - Convolutional Networks (CNN)

• 그래프를 convolution함수를 통해 계산하는 방식 (Text / Image)
• 문제점
  • Graph에는 고정된 지역성(locality)이 없다.
  • 고정된 윈도우(window) 크기도 없다.
  • 순열이 불변(Permutation Invariant)한다

(1) Permutation Invariance란? 

• 그래프는 위의 그림과 같이 노드별로 명칭을 정한 후 인접행렬(adjacency matrix)의 형태로 표현할 수 있다. 
• But, 이름을 어떻게 붙이느냐에 따라서 인접행렬(adjacency matrix)의 형태가 판이하게 달라진다.
  • 이때, 명명하는 순열(Permutation)에 상관없이 모든 쌍(ex. order_1 ↔ order_2)은 같은 정보(node representation)을 표현한다. 
  • 즉. 순열에 관계없이 함수 f(A,X)가 같은 결과값을 반환한다.  
• 때문에 순열에 관계없이 함수 f(A, X)가 같은 결과값을 반환하는 함수를 Permutation Invariance function이라 한다.
  • f(A_i, X_j) = f(A_j, X_j) 

(2) Permutation Equivariance란?

• 위의 그림과 같이 노드는 다양한 순열에 따라 명명할 수 있다. 
• 하지만 명명에 관계 없이 동일한 노드를 가리키는 명명간에는 동일한 이웃(neighborhood)정보를 포함하고 있다. 
• 때문에 순열에 관계없이 함수 f(A, X)가 같은 pair의 순서쌍을 나타내는 함수를 Permutation Equivariance function이라 한다.

3) Graph Neural Network Overview

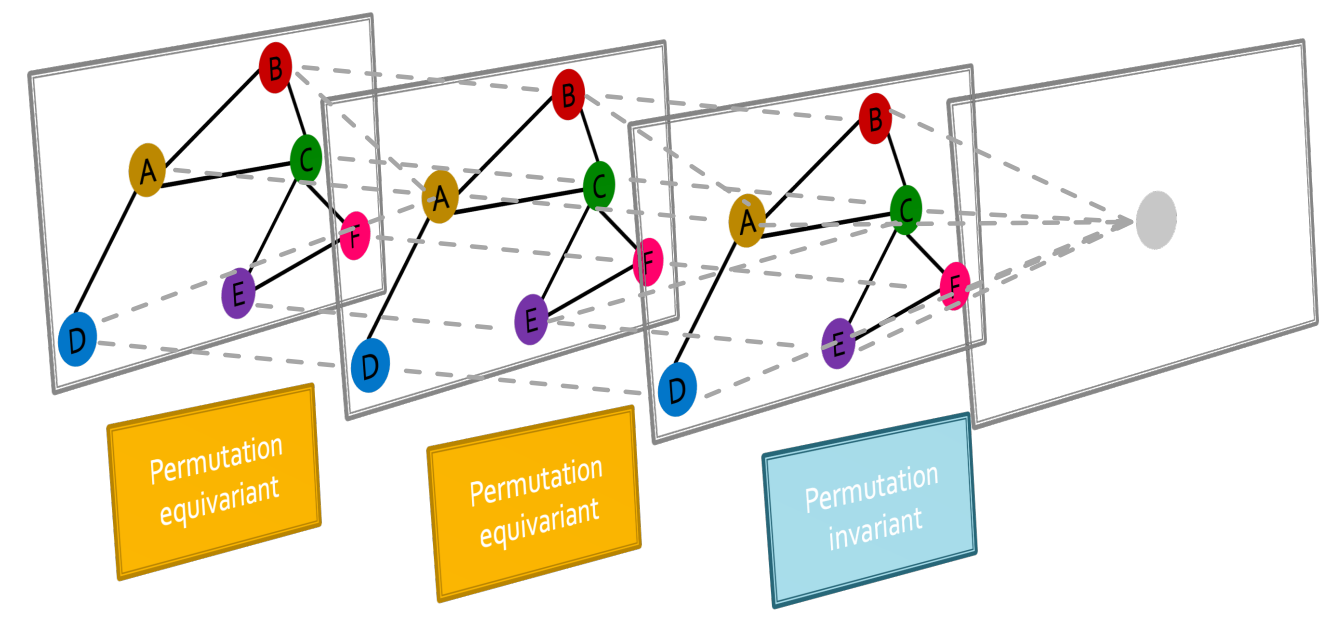
• GNN은 여러쌍의 multiple permutation equivariant / invariant function들을 포함한다.
• 이는 다른 MLP들과는 구별되는 특징이다.
  • 다른 DNN모델들은 데이터의 순서가 변하는 경우 값이 달라짐 
  • Ex. 홍김길철동수 ↔ 김홍철길수동

---

2. GCN: Graph Convolutional Networks

• 개념: 노드와 이웃들의 관계를 기반으로 Computation Graph를 정의해보자
• 목표: Node feature를계산하기 위해 graph에서 정보가 어떤식으로 전파되어가는지 확인한다.
• 기타 설명: 위의 그래프는 depth가 k=2만큼인 Tree구조로도 볼 수 있다. 

1) 아이디어1 - Aggregate Neighbors

• 핵심 개념: 
  • 근접 이웃 네트워크(local network neighborhood)를 기반으로 임베딩을 생성한다.
  • 각 노드들의 정보를 Neural Networks를 통해 결합한다. 
    • 즉, Target Node와 연결된 모든 이웃들의 임베딩을 다시 NN을 통해 결합(Aggregate)하여 Target Node의 임베딩을 산출하는 방식
    • 이때, 이웃 노드들의 임베딩 또한 연결된 모든 노드들의 정보를 결합(Aggregate)하여 생성

(1) 특징1 - Computational graph 

• 모든 노드들은 이웃들을 기반으로 각각 Computation Graph를 표현할 수 있다. 

(2) 특징2 - Deep Model (Many Layers) 

• 모델은 임의적인 깊이(arbitrary depth)를 갖는다. 
  • Layer-0 임베딩은 input feature인 x_v이다. 
  • Layer-K 임베딩은K hop만큼 떨어진 정보를 지니고 있다.
    • 즉, K번 aggregate된 정보를 지니고 있다. 

(3) 특징3 - Neighborhood Aggregation

 

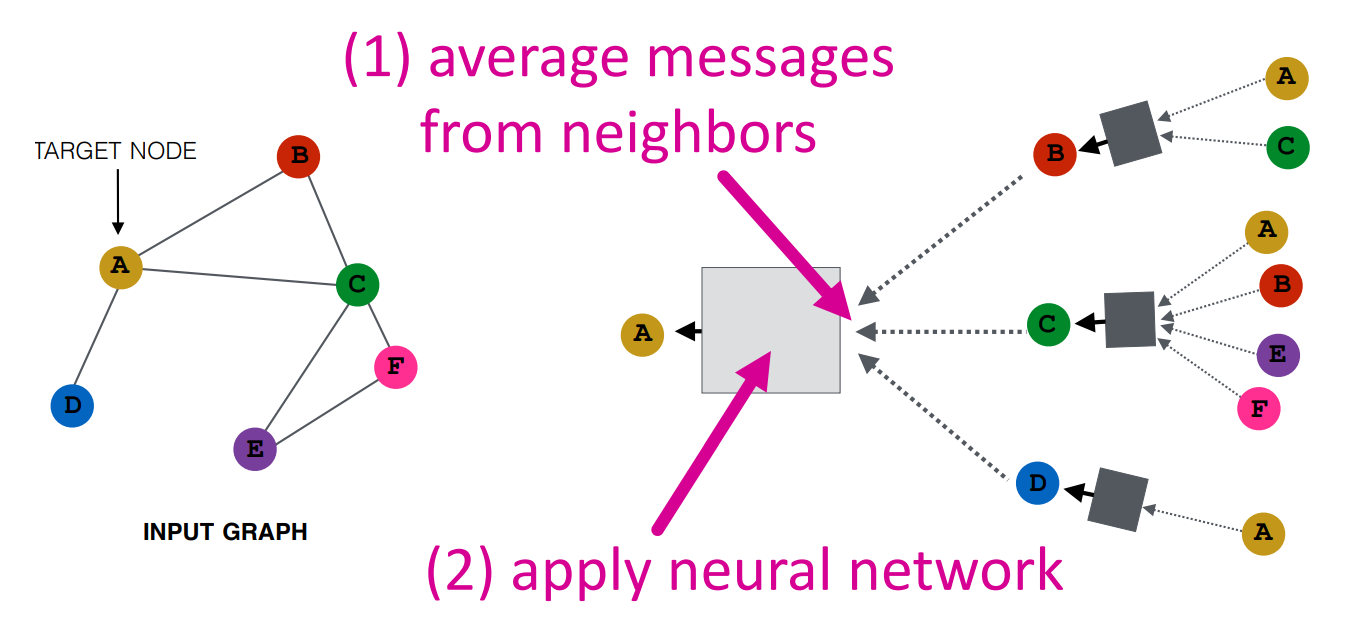
• Information을 얼마나 다양한 방식으로 결합할지가 중요하다. 
• Basic Approach:
  • 1) 이웃 임베딩들의 정보를 평균낸다. 
  • 2) 이 정보들을 NN을 거쳐 계산한다.

(4) K번째 Embedding 계산 공식 

• h0: 최초 h0 임베딩은 node feature와 동일하다.
• z = Neighbor Aggregation의 결과로써 나온 임베딩 z는 h와 동일하다. 
• sigma = 활성화 함수를 나타낸다. (e.g., sigmoid, ReLU 등) 
• K = 전체 Layer의 개수를 나타낸다. 
• h(k) = k번째 layer의 임베딩을 나타낸다. 
• ∑h(k)_N(v) / |N(V)| = k번째 노드 v의 이웃 노드 임베딩들의 평균이다.\ 

• W_k = 이웃 노드 임베딩들의 정보에 대한 학습 가중치이다.
• B_k = 자신 노드 임베딩에 대한 학습 가중치이다. 
• W_k와 B_k는 학습 가능한 파라미터이다. (Trainable parameter)
• SGD방식을 통해 파라미터를 학습할 수 있다. 

---

3. CNNs과 Transformers를 포함하는 개념인 GNNs

(1) CNN - Convolutional Neural Networks 

• CNN은 fixed neighbor size와 fixed ordering을 가진 GNN으로도 볼 수 있다.
  • CNN은 filter 사이즈가 pre-defined되어 있다. 
  • GNN의 장점은 각각의 node들에 대해 각기 다른 임의의 depth를 가진 그래프를 계산할 수 있다는 점이다. 
• CNN은 순열 불변(Permutation equivariant)하지 않다. 
  • 픽셀들의 순서를 바꾸면 다른 이미지가 된다. 

(2) Transformer - self-attention

• Transformer는 Sequential 모델링에서 많이 쓰이는 구조이다. 
  • self-attention은 Token들간의 모든 관계를 포함한다. 
  • self-attention이 다른 모든 단어들과의 관계를 참조하기 때문에 fully-connected-"word"-GNN으로도 볼 수 있다.